Turing and the Poker Endgame

Before Alan Turing designed a machine to crack the Nazi enigma code, or laid the foundations for artificial intelligence, he was an exchange student at Princeton University. He was there to study logic and computation, but also had the chance to attend other lectures—like the one given by mathematician John von Neumann in March 1937, on the theory of games.
Von Neumann’s work had started with a simplified version of two-player poker. Each player put in an ante of $1 then received a single card, which displayed a random number between 0 and 1. The first player could then choose to check—which forced a showdown—or bet, in which case the second player could choose to call or fold. Let’s suppose the game is pot-limit. The decision process for player 1 and player 2 can therefore be sketched out in diagram #1.
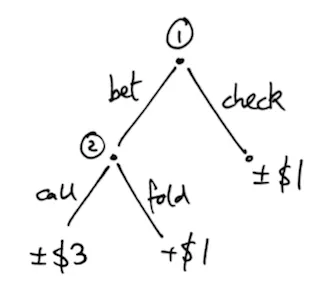
The dollars at the bottom of each branch show the potential profits for player 1. If the game ends with a call or a check, the winnings will depend on whose card is higher. But what is the best strategy for this game?
In poker, both players are trying to minimize their opponents’ profits. In 1928, von Neumann proved that in such games there would always be an optimal strategy for each player—this would guarantee them the best possible outcome, assuming their opponent was trying to do the same.
For the game above, von Neumann found that the optimal strategy for player 1 is to bet if they are dealt a card with a value greater than 14/18—or if the value is less than 2/18. In other words, the math says they should bluff if they get dealt a very bad card. In response, player 2 should call a bet only if they have a card with a value above 10/18, and fold otherwise. Even so, the game isn’t completely fair: If both players adopt optimal strategies, player 2 will lose $2/18 (or about 11¢) per hand on average.
Turing plays poker
Von Neumann’s research certainty left an impression on Alan Turing. In the late 1940s, Turing started to write a paper on ‘The Theory of the Correct Strategy for Playing Two-man One-card poker’. From the notes that survived after his death, it seems that his main criticism of von Neumann’s version of poker was the lack of betting rounds. ‘The restriction in the raise is an admitted blemish on the theory,’ Turing noted.
Turing tried to tackle a version of the game in which two players could raise and re-raise as many times as they liked. He made some inroads in the analysis, suggesting—as von Neumann did—that players should sometimes bluff with weaker cards. However, according to the notes he left behind, he did not find a full strategy for the game.
Refining von Neumann’s poker
The optimal strategy for two-player poker has continued to intrigue theorists. In 2007, poker pro, Chris Ferguson published a paper in Game Theory and Applications along with his father Thomas, a math professor at UCLA, and mathematician Céphas Gawargy. Unlike Turing, who allowed multiple betting rounds, the trio focused on a more basic extension to von Neumann’s game. As before, each received a single card, with a value between 0 and 1. But this time, the second player could respond to a check by player 1 either with a bet or check. The decision tree therefore has an extra branch on the right-hand side as noted by diagram #2.
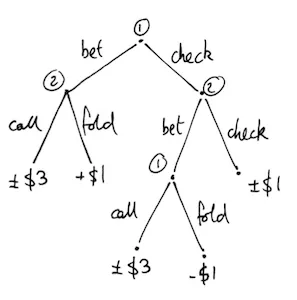
What’s the optimal strategy for each player in this situation? Ferguson and his co-authors found that player 1 should again bet with a low or high card, and check otherwise. If player 1 bets initially, player 2 should call if they have a high card and fold if not. If player 1 checks, player 2 should also bet with a high or low card, and check with a middling one.
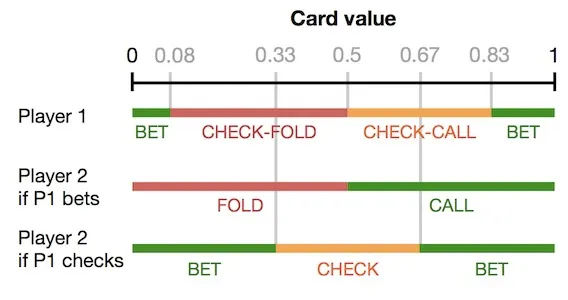
We can summarize the strategy for each player by dividing the region between 0 and 1 into intervals that specify what a player should do if they have a card with a value in that range (see diagram #3).
For example, if player 1 opens by checking and player 2 has a card with a number less than 0.33, player 2 should respond by betting.
Poker artificial intelligence
Real two-player poker games—like heads-up no-limit hold’em—are too complicated to calculate an exact optimal strategy. As a result, the best computer bots usually try and approximate the ideal strategy, by simulating billions of hands and refining their approach as they learn what works and what doesn’t. However, there is still a role for the stripped-down versions of poker pioneered by von Neumann.
Last year, researchers at Carnegie Mellon University in Pittsburgh, PA pitted their heads-up no-limit hold’em bot against poker pros Dong Kim, Jason Les, Bjorn Li, and Doug Polk. Although the bot used an approximation of the optimal strategy for the majority of the game, as each round approached its conclusion it switched to an ‘endgame’ strategy, which looked at all possible options left, and identified the best strategy given the available information. Whereas human players often count their ‘outs’ as a hand progresses, the Carnegie Mellon bot was able to crunch through every possibility.
It proved a highly effective strategy. In a paper reflecting on the competition, Sam Ganzfried, one of the researchers on the project, said Polk told him afterwards that ‘the river strategy of Claudico using the endgame solver was the strongest part of the agent’. Indeed, endgame analysis has already helped computers beat humans at checkers and chess. As Alan Turing once said, ‘we may hope that machines will eventually compete with men in all purely intellectual fields.’
Could no-limit poker be next?
Discover more about the science of gambling with The Perfect Bet: How Science and Math are Taking the Luck Out of Gambling.
*advertisement*










