Alec Torelli’s “Hand of the Day”: Could You Fold a Full House?

Alec Torelli is a poker professional originally from California, but travels the world full time with his wife, Ambra. Torelli has over $1.5 million in live tournament earnings (including two World Series of Poker final tables and two World Poker Tour final tables) as well as over $500,000 in online tournament earnings. Outside of poker he and his wife manage a million-dollar online business which travels the world with them.
In Torelli’s “Hand of the Day” series he analyzes hands played by him and submitted to him by others. Today he reviews a cash game hand sent in by a reader finding himself in the unusual spot of having to decide on the river whether or not to fold a full house.
This new “Hand of the Day” comes from a reader, Etan, who while playing a $1/$3 no-limit hold’em cash game found himself in an interesting hand resulting in a difficult river decision. Take a look at the video, then continue below for some further analysis of the hand.
To go over that hand history again, it’s a full ring $1/$3 live NL game, with $400 effective stacks. Five players limp, Hero raises to $20 from the button (large for the game) with A♣A♠, and the SB and one other player call, making the pot $73.
Flop: Q♠8♠2♠
SB leads for $35, other player folds, Hero raises to $110, SB calls. Pot $293.
Turn: 2♣
SB checks, Hero checks.
River: 2♦
SB shoves for $250, Hero calls. SB shows 8♦8♣, wins.
Analysis
Jumping to the river decision, the pot on the river is almost $300 and our Hero needs to call another $250, making his odds 550-to-250 or 2.2-to-1. This means he’ll need 32% equity to break even on the call. Are there enough combinations of hands that his opponent could have (given how Villain played the hand) against which Etan would have more than 32% equity? Put simply, does the Hero here have > 32% equity vs. Villain’s range?
Before we look at the math, let’s do a quick breakdown of the Villain’s range.
Prefop: Playing from the small blind, the Villain (a good, solid player) called the raise by the Hero (who is also a good, solid player). He clearly has a playable hand and his range is something like mid-pairs to Jx10x-suited or better, depending on how loose he is. The likely best hand he can have is JxJx or AxQx-suited, as most players would three-bet QxQx+ and AxKx here.
Flop: Villain led out and called a raise on the flop. This removes bluffs entirely from his range (one of the reasons I dislike raising the flop) as well as many one-pair combos which we beat like QxJx or maybe even KxQx (another reason I dislike raising the flop). In other words, his range now is AxQx, sets (8x8x, 2x2x), and flushes. He cannot have bluffs because there are no offsuit combinations with which he can call preflop and then call the flop (KxJx-offsuit folds preflop, for example).
Turn: Both players check. No new information is gained, as we assume the Villain checks 100% of his range here on the turn.
River: Villain bets $250. We can remove all flushes from his range — it would be an insane value bet, and his hand is too strong to turn into a bluff. Since he can have no bluffs on the flop, his range is now comprised only of full houses, specifically AxQx and 8x8x.
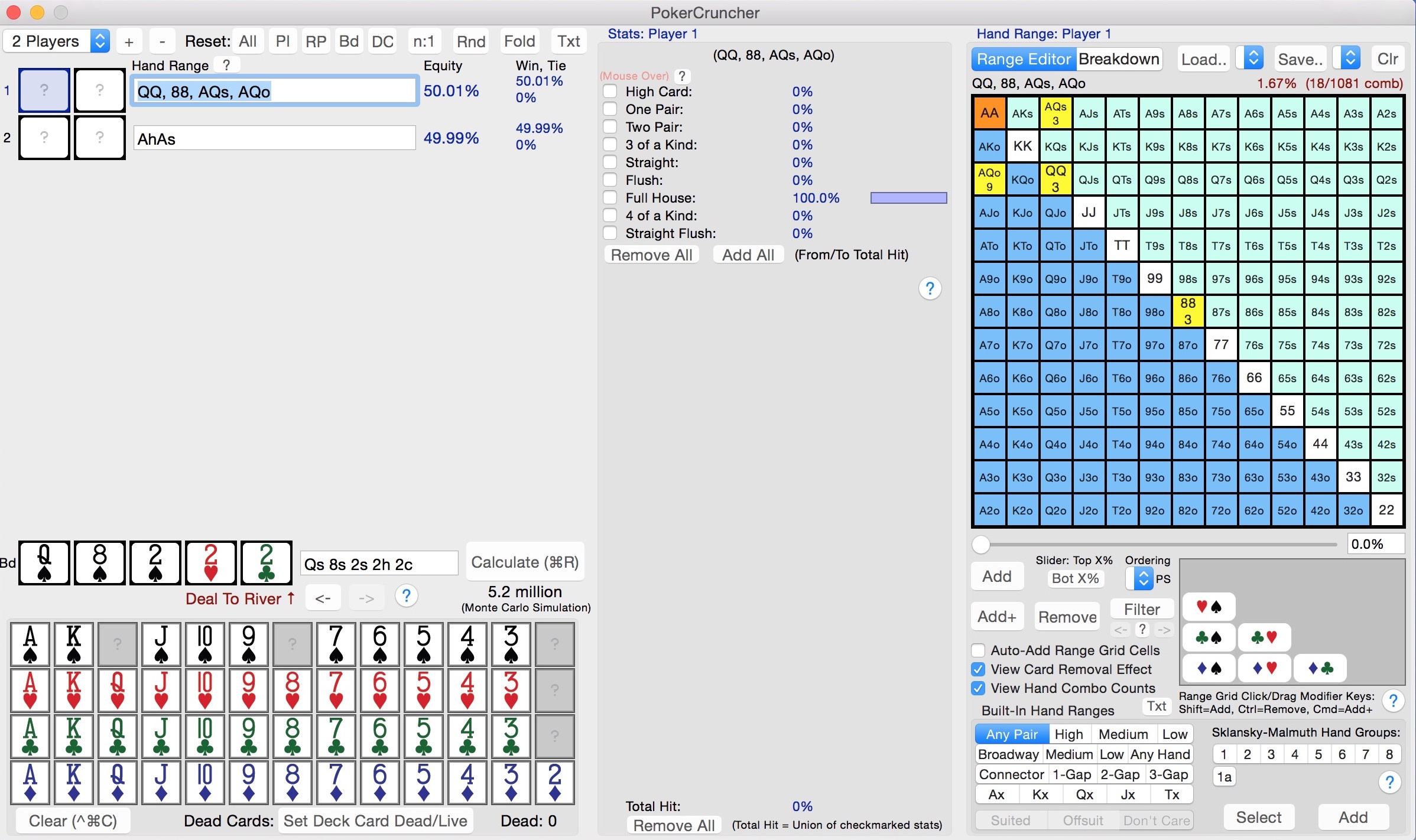
I always like to be conservative when doing range analysis, giving my opponent more hands which can beat me and less which I beat. In doing so, I’m certain that if I still have enough equity to call, then a call must be a clearly profitable play.
As you can see I removed KxQx from his range entirely (a hand which I beat) and added QxQx into his range (a hand which beats me that is very unlikely which the Villian holds). In doing so, I still have 50% equity vs. his range. Since I only need 32% to justify calling, this is a clear call. And empirical data at a $1/$3 game confirms this — unless you have an epic read or know your opponent extremely well, you’re just not beat here often enough.
How do you go about figuing this out on the spot? By counting combos.
- AxQx: 6 combos (you have two aces, and there’s a queen on the board)
- QxQx: 3 combos
- 8x8x: 3 combos
- Win: 6/12 = 50%
But what if he doesn’t value bet shove with 100% of his AxQx combos? Fine. Let’s say he only shoves AxQx 50% of the time. Instead of winning 6/12 you win 3/9 = 33%, and you would break even at worst.
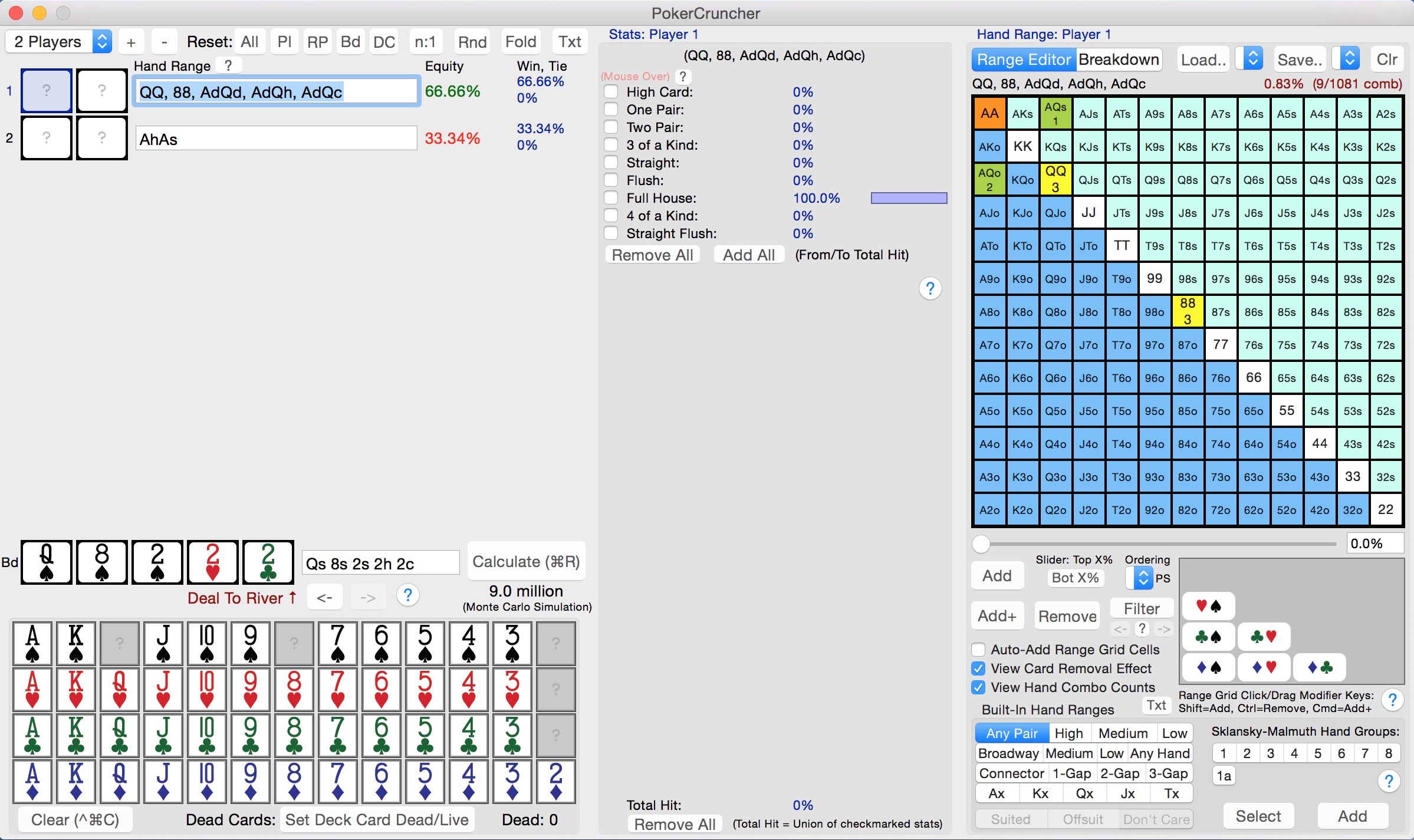
Another way of looking at it is to ask the following: How many hand combos would he need for you to fold? Since 3 combos are enough to break even — remember, we are being hyper-conservative assuming he has QxQx 100% of the time, which is impossible — he would need never to have more than 2 combos of hands worse than ours.
Conclusion
Translation = you cannot fold the river. Ever. What would you have done? Leave your thoughts in a comment below.
Also, as I announced at the beginning of the video, I have a new show out called “#HelloAlec” in which readers send in hands that will be read and analyzed by my friend, the robot, on a new YouTube channel. The best ones will be selected each week to be featured in the following week’s “Hand of the Day.” You can see more about it by clicking here.
Want to be featured on future episodes of “Hand of the Day”? Simply submit your hands to Alec here. Also check out “AskAlec,” a new series on YouTube where aspiring poker players can send in their questions and get feedback.
Follow Alec Torelli on Twitter, Instagram, through Facebook, or via his popular blog.
Get all the latest PokerNews updates on your social media outlets. Follow us on Twitter and find us on both Facebook and Google+!










