Understanding Why We Are Betting; or, Poker Pundits Can Be Wrong

I recently read a hand history analysis by a well-known poker pro with which I emphatically disagreed. Such disagreements aren't unusual since there are often multiple ways to perceive a poker problem. But it struck me how easy it is simply to accept whatever advice we happen to read — especially from a poker pundit, and even more especially when it contains common poker clichés.
Instead, the key to poker improvement is to look at all poker advice critically, including my own.
The Hand Example
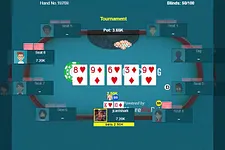
Our Hero was playing in a Vegas $2/$5 game with $400 effective stacks. A solid "ABC" player opened to $15 from the cutoff and Hero had 10♠9♠ on the button. Thinking that Villain would fold a big fraction of his opening range to a raise, Hero reraised to $50. The villain called, creating a $102 pot after his opponent called (and after the rake).
The flop was 10♥8♠3♠ and Mr. Villain checked. Hero bet $85 and Villain folded.
This seems like a fairly straightforward hand, and it is. But the reasoning behind Hero's decision-making invites discussion.
Preflop Analysis
The average Vegas $2/$5 player makes a preflop raise about 8 percent of the time. Since Mr. Villain is a solid player opening in the cutoff, we could assign him a wider opening range than that.
Suppose he opens with a 12.8 percent range, which according to Flopzilla would be [22+, AK, AQ, AJ, KQ, KJ, QJs, JTs], which is 170 combos. With Hero's hole cards removed, this is reduced to 162 combos, or a 12.2 percent range.
Mr. Hero believes that Mr. Villain would defend against a three-bet with [88+, AK, AQ, AJs, KQs], which is 82 combos and a 6.2 percent range. With card removal, this makes 76 combos, or a 5.7 percent range.
Accordingly, Hero expects his Fold Equity (FE) to be 86/162 = 0.53, with Pot1 = $22. (We'll assume for now that Mr. Villain never four-bets.) His Equity-When-Called (EWC) is 0.332 with Pot2 = $102 after the rake. So we have:
- EVBet$50 = (FE) × (Pot1) + (1-FE) × (EWC × Pot2 – 3BetSize) = +$4.11
So Hero's $50 three-bet appears to be a profitable play in this specific situation. However, we have not considered that this EV would decrease if Mr. Villain four-bets with some of his range, inducing Hero to fold. In this case, we have EV4Bet = +$2.49. If Mr. Villain four-bets with queens and ace-king often enough, and if Hero always folds, Hero's three-bet might actually be unprofitable!
Additionally, this EV also only reflects Hero's showdown equity, which does not consider how the hand might play out postflop, which is a function of Hero's skill and position. And Hero's EV could be better if Mr. Villain's opening range is wider or if his three-bet calling range is tighter.
This analysis doesn't necessarily make a $50 three-bet Hero's best play. Flatting or three-betting a different amount might be superior.
Suppose Hero raises to $40 instead of $50. If we assume Mr. Villain's defending range is the same for both, we have EVBet$40 = $5.69 if Mr. Villain never four-bets. If Mr. Villain four-bets [KK+], folding out Hero, his EV4Bet = +$3.67. This implies that the smaller three-bet is more profitable in either scenario.
Flatting would make the pot $33 (after the rake). But Hero is now facing Mr. Villain's full 12.8 percent range. This generates 38.83 percent showdown equity with an EV of $12.81. Considering Hero's $15 investment, this has a EVCall$15 = -$2.19. Therefore, calling is inferior to folding or three-betting.
There are enough uncertainties in this analysis that we can't say for certain whether a $40 three-bet is superior to the $50 bet. Each bet is reasonable, and Hero's EV for the hand will depend on how it plays out postflop.
But I prefer the smaller three-bet because it has a slightly better current EV. It risks less when raised, and it allows Mr. Villain to auto-continuation bet when he misses.
Flop Analysis
The 10♥8♠3♠ flop is good for Hero, who makes top pair, weak kicker with his 10♠9♠. Since Mr. Villain did not four-bet, Hero eliminates both AA and KK from his range, leaving him with [88-QQ, AK, AQ, AJs, KQs], which is 64 combos (5.2 percent). With card removal, Mr. Villain has only 59 combos (4.5 percent) on the flop.
Hero is only behind 16 of these combos, the sets and overpairs. Since there are no tens in Mr. Villain's three-bet calling range (except for pocket tens), the strength of Hero's kicker is nearly irrelevant.
Since the villain is a solid ABC player, his flop check does not narrow his range. Hero has the best hand 43/59 = 73 percent of the time. If Villain folds every inferior hand to a continuation bet, Hero's Equity-When-Called is only about 20 percent. However, a solid ABC player may well check-raise his overpairs, forcing Hero to fold most of the time.
Hero bets $85 into the $102 pot. If Villain folds every inferior hand and never check-raises, Hero's bet is not immediately profitable. He must rely on his Equity-When-Called to make up the difference. So 73 percent of the time he wins the $102 pot, which means he has risked $85 to win $74. If Villain pushes Hero off the hand the other 27 percent of the time by check-raising, Hero's continuation bet is a –EV play.
But if Villain never check-raises (not likely by a solid ABC player), Hero's $85 bet will be +EV because he will gain some additional value from the showdown equity of his hand.
Hero's Thought Process
Hero chose to bet large because he thought Mr. Villain "would fold any overcards," adding "this would define his hand and narrow his ranges for my turn and river decisions, making them easier."
This may be true, but it isn't what Hero should be trying to do. He has a value hand only when his Value Bet Ratio is greater than 1.0. He should want his opponent to call with his inferior overcards, not fold them. Each overcard has only three outs, creating merely a 6 percent chance on the turn card. Hero should want Mr. Villain to pay a dear price for the opportunity to chase.
Hero also wants to remove some of his postflop decision-making stress. He puts an emphasis on winning the pot immediately, since it already has significant money in it. Hero also thinks that since the EV of most future bets would be close, the value of any missed bets wasn't much to give up.
Many weak players think like this, but the logic is faulty. As the superior player in superior position, postflop complexity is Hero's friend. He should be battling for every dollar of extra EV.
Bet Sizing
Hero had previously seen Mr. Villain call a 40 percent-pot bet with AxQx-suited on a low board after being three-bet preflop. So he has reason to believe that a $50 bet in this situation would get a lot of calls from inferior hands.
In fact, Mr. Villain might call with all of his inferior hands, including AxJx-suited, AxQx-offsuit, and 9x9x. This would provide Hero a Value Bet Ratio of 43/16 = 2.7, which would be a very profitable value bet. Even if Mr. Villain calls with only half of his inferior combos, Hero's VBR is still a very healthy 1.35.
Another way to look at the bet sizing question is to note that a larger continuation bet makes it more likely that Mr. Villain will make the best play (folding). A smaller bet increases his likelihood of making a mistake. The optimum bet size is the one that makes the most money in the hand. I think the smaller $50 bet has a better chance of that.
On the Turn
Hero is obviously worried about seeing an overcard on the turn. He is willing to distort his play in order to avoid this. But should this be a big concern for him?
The chance that an overcard will hit the turn is only 16/47 = 34 percent. This is even less likely if Mr. Villain holds two overcards (14/47 = 30 percent). Although 36 out of Mr. Villain's 59 combos (61 percent) have an ace, there is only a 3/47 = 6.4 percent chance that the turn would bring a second one. So there is only a 0.61 × 0.064 = 3.9 percent chance that the turn will bring a bad ace for Hero.
Furthermore, only 20 of Mr. Villain's combos have a king, 26 of them a queen, and 10 of them a jack. Overall, Hero shouldn't be overly worried about the turn card. When an overcard hits, he can use his superior position and skill to maximize his wins and minimize his losses.
You should study my analysis, compare it to the pro's analysis, or come up with your own. Any or all of us could be mistaken. But the analytical process will make you a stronger player in the long run.
Steve Selbrede has been playing poker for 20 years and writing about it since 2012. He is the author of five books, The Statistics of Poker, Beat the Donks, Donkey Poker Volume 1: Preflop, Donkey Poker Volume 2: Postflop, and Donkey Poker Volume 3: Hand Reading.