Game Theory Optimal Solutions and Poker: A Few Thoughts on GTO Poker

The 'GTO' part of GTO poker stands for 'game theory optimal.' In poker, this term gets thrown around to signal a few different concepts.
GTO refers to thoughts about opponent modelling, and thinking about poker situations in terms of ranges and probabilities, as opposed to being strictly results-oriented.
Sometimes those ideas get reduced to young pros shouting across a poker room (or the Twittersphere, as you can see on the PokerNews Twitter tracker) about whether a given play is 'GTO' — or even 'the opposite of GTO,' as I recently saw in a discussion thread.
But what does GTO poker really mean? And does it apply to your game?
Seeking an Unexploitable Strategy
A game theory optimal solution to a game has precise mathematical definitions.
It is interesting to consider what this means to a poker player, as well as how this concept has become a dominant framework for looking at ideal poker strategy.
Since most of my time these days is spent building computer AIs that play strong poker, I'm often thinking about how computers look to GTO poker strategies for playing unexploitable poker.
GTO — especially in the context of modern poker games — is largely about pursuing a strategy that makes it impossible for you to get pushed around.
Think Uma Thurman in Kill Bill. Or Bruce Willis in any Bruce Willis movie.
Outside of poker, GTO is usually introduced with the "prisoner's dilemma."

In this hypothetical situation, the two of us are arrested for jointly committing a crime.
If neither of us talks, we both get off with light sentences. However, if one of us snitches on the other, the snitch will get off with no punishment at all, while the person who doesn't talk gets a harsh sentence.
If we both snitch, we both get a harsh sentence, since each person's testimony can be used against the other.
Even though we would be best off with the first scenario (nobody talks), each individual is better off from collaborating with the authorities, regardless of what the other does (if I don't snitch, you should snitch to get off free, and if I do snitch, you should definitely snitch as well).
In an environment where players are rewarded for taking advantage of each other, it may not be worth acting cooperatively, even if all sides would be better off by doing so.
The 'Bubble Dilemma'

The poker equivalent would be two players fighting it out on the bubble of a tournament.
Except for the super-deep stacks who can chip up on the bubble with no risk of busting, the remaining players benefit from any confrontation that leads to elimination.
Thus the two players in the hand are only hurting themselves, by trying to bust each other. And yet, it's not possible for them to collaborate toward a mutually beneficial solution.
Reacting to an opponent's attempts to run you over is so natural to a thinking poker player, framing it in terms of GTO poker can seem almost superfluous.
Of course your opponent has a strategy. You have some idea of what that strategy would be with various hands, and your job is to take that into account when executing your own strategy.
In other words, play the player. This is what GTO poker is all about.
The Quest to "Solve" Hold'em (and Other Games)
As you adjust your strategy to an opponent's strategy, he or she will adjust to yours, and so forth.
For heads-up limit Texas hold'em, the University of Alberta team took this process to its logical conclusion, publishing their results earlier this year in Science magazine.
Using a network of computers, they set two strategies loose, repeatedly adjusting to each others' play.
Eventually, they reached a state where neither player could gain even a 1% advantage against the other in any specific situation.
This sounds complicated, and I'm simplifying what they did slightly. But in essence, they reached a strategy which an opponent cannot exploit — or at least cannot exploit beyond a 1% edge — with any other possible strategy.
Somewhat confusingly, the University of Alberta team claims both to have "solved" heads up limit hold'em, and also that they found just one GTO equilibrium for heads-up limit hold'em, and that there are likely to be other equilibria for the game, left to be discovered.

According to the paper, their "near perfect" heads-up limit hold'em bot raises 90%+ of hands on the button, but doesn't four-bet when it gets three-bet from the BB almost at all, even with AxAx.
This seems to imply that four-betting AxAx on the button is wrong, or at least not as profitable as is disguising the hand by flat-calling the three-bet.
The first time I read their paper, that's certainly what I thought they meant.
However, the Alberta folks are quick to point out that calling a three-bet with AxAx on the button 100% of the time is only optimal in the GTO equilibrium that they found.
Given the rest of their strategy, it would be worse to four-bet with pocket aces. You probably could four-bet with aces, but then the rest of the strategy would need to adjust.
At the very least, you'd need to four-bet other hands, too, so as not to give it away that you had aces. If they fixed AxAx as a four-bet and ran the rest of the process until it stabilized, would it reach a different GTO equilibrium? That would be an interesting experiment.
In practice, if you know that your opponent will call off with one-pair hands against pocket aces, and not react as though he knows your very tight four-betting range, then you're just missing a bet.
In an episode of The Thinking Poker Podcast, Andrew Brokos and Nate Meyvis explain this point well.
Game theory uses a strong definition of optimal play, where you're supposed to consider every play you would ever make with any hand as part of the equilibrium.
However, in real cases, 95% of that is optimizing for what you would do in this spot, given the range of hands that you could be playing, and what your opponents' hands might be.
In a hand discussed on the show, a listener in a limit hold'em game held KxKx out of position on an ace-high flop.
Heads-up, this is still a plus-EV hand, but there isn't much value in betting. You're not getting an ace to fold, and by checking, you'll get more value from a bluff, as well as from a value bet with middle pair.
Let's think about this situation as a computer AI might.
Say you're playing $100/$200 limit hold'em. The pot is $400, and you raised preflop with KxKx.
Your hand's value might be something like +$700 at this point (including the odds of winning the pot, and the value of future bets). Now the ace flops, and your value drops to +$300 or so.
More importantly, the value of check-calling might drop by less than then the value of betting out.
Estimating the value of your hand, assuming that both players play well and about even in the long run, is just another way of approximating GTO.
READ ALSO: The 10 Most Important Poker Strategy Books Ever Written and Why They’re Special
When Everyone Knows What Everyone Else Is Doing
Once you're in three-handed (or more) games, there is no game theory optimal solution, strictly speaking.
This is because there is no stable equilibrium (or too many equilibria to count, depending on whom you ask).
The players can always adjust to each other, or take advantage of a player trying to execute a GTO poker strategy and not adjusting to them, through a process that Bill Chen and Jerrod Ankenman call "implicit collusion" in their 2006 book The Mathematics of Poker.
Thus there is no unexploitable strategy.

Let's dig into this for a second.
When playing heads up, if you (or a bot) follows a GTO poker strategy, an opponent can't beat you in the long run, no matter what he or she does.
This does not mean that you are winning the most against this opponent, but you are locking in a long-term tie, while still benefitting from some of your opponent's mistakes.
For example, the limit hold'em GTO bot will pay off on the river with bottom pair often enough so you can't bluff it effectively.
If you never bluff in this spot, the bot will still pay you off at the same rate. An exploitative player would stop paying you off after a while, and win even more.
Poker pro and poker training site founder Doug Polk spoke on the TwoPlusTwo Pokercast about this situation coming up during a man-vs.-machine NLH match.
It was such a relief to the players once they realized that while the computer played well ("4 out of 10" compared to his regular opponents, according to Polk), it did not attempt to exploit their betting patterns.
If when you flop the nuts you bet 1.5x the pot or crumble a cookie, the AI doesn't know or care. It just plays GTO poker.
In an idealized 3+ player game where everyone adjusts to everyone, GTO should not work. But in practice, if the players don't change their strategies too much from hand to hand (and they don't), a lot of the heads-up Game Theory Optional principles apply.
A friend of mine went to graduate school with one of the best online poker players in the world, and had a chance to watch him play.
He was surprised that his classmate did not make any unusual plays, or really any "moves" at all. According to the poker pro:
- everybody knows who I am
- everybody knows how I play
- there's no reason to get out of line
If you take Chen and Ankenman's ideas about "implicit collusion" to heart, one could also add that if the players were ganging up on him instead of trying to beat each other, the pro would just quit the game.
This is a non-issue in the nosebleed games, since everyone knows everyone else, and playing anonymously or collusively isn't really possible.
The point is, the best players in online poker play GTO. They must be really good at knowing when to bet 80% of the time and to call 20%, and when to call 20% and to fold 80%. And then they actually do it.
There's a lot to be said for good execution. (I tend to find that 20% call button a little bit too often.)
It's also easy to see why Polk in the same interview is pessimistic about humans' chances, once the bots learn all the right bet frequencies.
Our silicon friends will always have that edge in execution, and they don't need room, food, or beverage.
Conclusion: GTO Poker is the Baseline
In the short term, the humans are converging on GTO more quickly.
When I sat in the stands in the Amazon Room at the Rio All-Suite Hotel and Casino for the final table of the $1 Million Big One for One Drop, it shocked me how loose-passive the play became after getting down to three-handed.
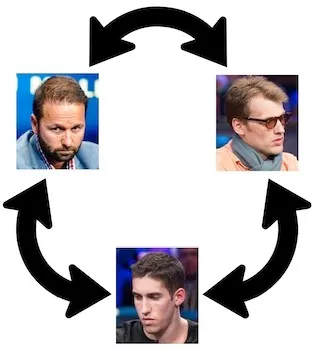
I took some flack on Twitter for comparing the small-bet, check-down game happening between Daniel Negreanu, Dan Colman and Christoph Vogelsang to a nightly satellite at a local casino.
Folks fired back that these guys are the best poker players in the world, and I'm clearly an idiot.
But it sure did look like none of the players were trying to pressure the others. And why should they? With payouts of $15M, $8M, $4M, there was a lot less upside in winning chips than was the downside to chipping down or busting.
On other hand, if one guy pushed, he knew the others knew how to fight back. So nobody pushed.
For about two hours, three of the best short-handed NLHE players in the world checked or small-bet every hand, until Vogelsang, the short stack, busted.
Do you need to play poker GTO in order to win? Or rather, how close do you need to get to optimal poker game theory in order to hold your own against a strong set of opponents?
Let's let Professor Tuomos Sandholm, head of Carnegie Mellon's Claudico no-limit hold'em team, answer that question.
In a recent article in Cigar Aficianado interviewing academics and enthusiasts at the Annual Computer Poker Championship, Sandholm was asked about his colleagues at the University of Alberta solving limit hold'em.
"They say it is essentially solved. I think that counts," responded Sandholm. "My question though is: was it essentially solved three years ago?"
Near-optimal poker GTO play is just the first step.
Once your baseline strategy can't be easily exploited, you can spend the rest of your time studying opponents' tendencies and adjusting to their weaknesses.
There will be plenty of opponents who don't think about ranges, who don't adjust to some of the game information, or who are just playing their own way.
Adjusting to them is what GTO, and poker, is really all about.
For a good, accessible exploration of how to use GTO in your game, check out Ed Miller's book Poker's 1%: The One Big Secret That Keeps Elite Players On Top .
Meanwhile for examples of how players use hand ranges to adjust to their opponents' strategies, see any of Alec Torelli's "Hand of the Day" analyses here on PokerNews, or this interview with Vegas $2/$5 NL pro Sangni Zhao.
A Quick GTO Poker Guide
What is GTO in Poker
GTO (or Game Theory Optimal) refers to an approach to the game of poker based on creating models about the players to then evaluate the game in terms of ranges and probabilities.
How does GTO work?
The GTO or Game Theory Optimal treats poker as a mathematical problem and uses analysis and calculations to 'solve' the game. The goal of this poker game theory is to lead a player to optimal play and make him impossible to beat.
How do I learn GTO poker?
A number of poker training sites offer courses and coaching programs to learn GTO poker.
As a beginner, you might want to use this article to start with poker GTO.
Is no limit hold'em solved?
Despite the University of Alberta claimed to have solved limit hold'em back in 2015, the models they have created still have numerous limitations.
According to former poker pro Doug Polk, advancements in AI and computing power could lead to bots solving the game of poker in a not too distant future.
This article was first published in September 2015. Last update: May 2020.
Nikolai Yakovenko is a professional poker player and software developer residing in Brooklyn, New York who helped create the ABC Open-Face Chinese Poker iPhone App.
Want to stay atop all the latest in the poker world? If so, make sure to get PokerNews updates on your social media outlets. Follow us on Twitter and find us on both Facebook and Google+!